The Fisher Index of Prices

The Fisher Index, sometimes called the Fisher Ideal Index, is a geometric average of a Laspeyres Index and a Paasche index. For details on those two types of price index, see the links below.

As a quick refresh, the Paasche Index suffers from the problem of underestimating inflation because it fixes a basket of currently consumed goods and compares its price today to what it would have cost in previous years. That doesn't account for the fact that consumers may well have preferred to purchase different goods in previous years, with the result that the index understates cost of living changes. For full details, see my article at: The Paasche Index.

The Laspeyres Index suffers from the opposite problem in that it fixes the representative basket of goods from a previous year and then tracks how its cost changes in subsequent years. This again fails to take account of peoples' desires to consume different baskets of goods as time passes, but in this index the result is an overestimate of the changing cost of living. For full details see my article at: The Laspeyres Index.

The Fisher Index attempts to improve on both these indexes by taking a geometric average of them both, thereby smoothing out the underestimates and overestimates.

The Fisher Index Formula

A geometric average of two values is arrived at by taking the square of both individual values and then multiplying them together. You then take that square root of that number:

Fisher Index Formula = √(Paasche² x Laspeyres²)

The Fisher Index, sometimes called the Fisher Ideal Index, may or may not be an improvement on the other two types of cost of living index, but it is far from perfect.

Why is the Fisher Index number called Ideal?

The Fisher Index is called ideal simply because it reduces some of the biases in the Paasche and Laspeyres indexes. It does not mean that it is an ideal index in the sense that it is perfect, because perfection is not possible. In the next section I will describe a perfect cost of living index, and from that you will see why such a thing is impossible to calculate in the real world.

A Perfect Cost of Living Index

In the graph below I will illustrate why the information requirements necessary for a perfect cost of living index are impossible to gather. I have used an indifference curve (in Blue labelled U) and two budget lines (in black labelled BL and BL'). For explanations of indifference curves and budget lines, see the links at the bottom of the page.

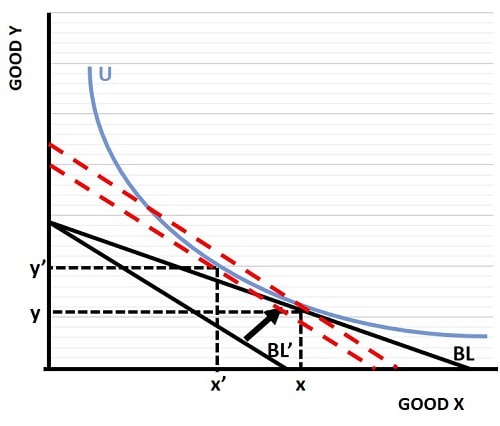
In the graph above we start with budget line BL, which represents all given quantities of two goods that can be afforded. The indifference curve belongs to a particular consumer, and represents his/her preferred combinations of the two goods. Naturally the indifference curve cannot be higher than the budget line because it would represent unaffordable combinations along all its length. The highest, and therefore satisfaction maximizing indifference curve, just touched the budget line at a single point.

That point represents the satisfaction maximizing combination of goods x and y. We call this the 'utility' maximizing point.

Now, assume that good x becomes more expensive. This results in a new budget line (BL') showing that fewer units of x are now affordable and that all combinations along the indifference curve are no longer attainable because it is higher than BL' at all points.

The two red dashed lines are drawn parallel to the BL' line. In order to compensate the consumer and reach an equal level of utility that was affordable before the price rise of good x, an increase in income is necessary to lift BL' up to the lower dashed red line. Notice that this results in a new preferred combination of goods with x' and y' the new preferred consumption bundle. Fewer amounts of x are desired because x is now relatively more expensive. However, since y is now relatively cheaper, more of y is consumed.

Since both x,y and x',y' both sit on the original indifference curve, both combinations are equally satisfying to the consumer.

However, a Laspeyres Index would suggest that an increase in income to allow an increased budget line equal to the lower dashed red line is insufficient, because that budget line does not allow the original combination of goods to be consumed. The Laspeyres Index estimates that a cost of living increase in income up to the higher dashed red line is necessary. Clearly this would be too much and would allow the consumer to consume along an entirely new (and higher) indifference curve that would more than compensate for the higher price of good x.

While not included in the graph, an illustration of the Paasche Index would show the opposite problem. The point is that the Fisher Index more or less reaches a midway point between the Paasche and Laspeyres errors; it can't reach an exact point because it is impossible to know exactly what any given consumer's indifference curve is.

In fact, every consumer has a different indifference curve as well as a different budget. So each person faces a different cost of living impact when relative prices change. Indifference curves and budget lines are just theoretical constructs used to highlight important concepts in economics, and in this case they demonstrate why the Fisher Index is not actually ideal. No perfect cost of living index is possible, and all of the main alternatives used have their strong points and their weak points.

Sources:

• General Information about Price Indexes (PDF)

Related Pages:

• The Indifference Curve
• The Budget Line
• Substitution Bias
• GDP Deflator vs CPI
• What if Inflation, and why is it Bad?

ShareFacebookXPinterestTumblrRedditWhatsApp