Intertemporal Budget Constraint & Choice

The Intertemporal Budget Constraint in economics looks at consumer choices over an extended time period when interest rates are earned or paid depending on whether a consumer prefers to borrow or save. The concept is sometimes called  'intertemporal choice' or 'dynamic choice'.

This is another one of those concepts in economics that the textbooks present with lots of off-putting mathematical equations, but the basic model is simple and should not cause the reader too much difficulty to grasp. In many ways the concept is treated as a sort of mathematical approach to the 'Permanent Income Hypothesis', as it provides models and graphs of consumption choices spread out over time.

As always, I'll keep the equations and notation to a minimum so as to avoid over-complicating the model, but it cannot be avoided completely. For simplicity, keep in mind the following:

• Y = Income (Y₁ is income today, Y₂ is income in the next time period)
• C = Consumption (C₁ is consumption today etc as with income)
• S = Saving (S₁ is saving today etc)
• r = the interest rate
  

Also for simplicity, assume that there are no surprises in future, so that a consumer knows what his/her income will be in the next time period and that our starting budget equals our starting income (i.e. we don't have any saved money or assets to fund our spending preferences). 

Finally, this is a basic two-period model (which it may help to think of as working-age period followed by retirement-age period), so any saving in the first period is spent in the next time period, and conversely any borrowing today is paid for in the next time period.

Note that any income that we save today will earn interest at a rate of r, meaning that our consumption in the next time period will be given by C₂ = Y₂ + S₁(1+r) and similarly if we borrow money in the first period then consumption will be reduced in the next period.

The Intertemporal Budget Constraint Formula

Next consider how to express consumption today and consumption in the next time period in terms of two equations. With a little thought we should understand that:

1. C₁ = Y₁ - S₁
2. C₂ = Y₂ + S₁(1+r)

Remember, this is a two-period model so any savings today will be spent in the next time period along with any interest that it earned. Now, with a little transposition of the first equation we can see that S₁ is equal to Y₁ - C₁, and if we plug that into the second equation instead of S₁ we get:

C₂ = Y₂ + (Y₁ - C₁)(1 + r), which can be written

C₂ = Y₂ + Y₁(1 + r) - C₁(1 + r)

Further rearrangement of this gives us C₁(1 + r) + C₂ = Y₁(1 + r) + Y₂

Finally, by dividing through by (1 + r)  we get the intertemporal budget constraint formula:

C₁ + C₂/(1 + r) = Y₁ + Y₂/(1 + r)

This is really just a convoluted way of showing us that the net present value of consumption over multiple time periods is equal to the net present value of income over those time periods. This is because income is equal to consumption plus saving, but saving must eventually become consumption because that is its whole point i.e., to fund future consumption.

Intertemporal Choice & Permanent Income Hypothesis

Each consumer will optimize his/her utility according to the interest rate, meaning that the extra spending power gained from the interest payment in future must be sufficient to compensate for having a reduced amount of consumption today.

If we imagine that period 1 is the working age period and that period 2 represents retirement, we may anticipate that Y₂ will be much lower than Y₁ and maybe even zero. In this case, given the permanent income hypothesis, we would expect people to save money throughout their working lives in order to be able to maintain a similar level of consumption during their retirement years.

Paradoxically, if this is true, then the higher the interest rate is the less saving will be required in order to maintain the level of consumption in retirement. This, however, seems unreasonable because a higher interest rate implies that saving is more rewarding in which case we might expect people to save a higher amount.

This is, of course, a false paradox. In practice people might well choose to save more as the interest rate increases, but they may also choose to retire sooner once their savings are sufficient to maintain a preferred amount of consumption. Also, the permanent income hypothesis needn't be interpreted too rigidly - some people may well prefer to enjoy a steadily increasing level of consumption over time rather than a constant level.

The point is merely that overall consumption is likely to be smoothed out over a lifetime, rather than sharply jumping up or down according to whatever income happens to be at any given moment.

Intertemporal Budget Constraint & Indifference Curves

I have previously explained indifference curves with respect to equally preferred combinations of goods in the two-good model (for a given time-period and budget constraint). The same analysis can be applied to multiple time-periods where a person must optimize his/her utility (satisfaction) by choosing between alternative combinations of consumption in the first period and consumption in a later period.

Continuing with our example of the first period representing a person's working-age, and the second period representing their retirement age, the graph below shows that the highest possible amount of utility is achieved by consuming x amount of goods during the working-age period, and y amount during retirement.

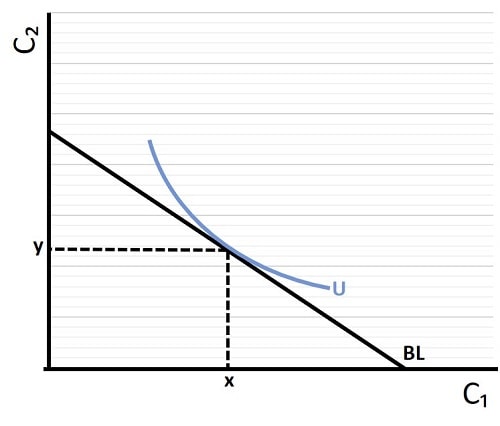
The straight black BL line represents the intertemporal budget line, it is a constraint because consumption above that line is not possible with the person's given level of income. We should also note that, since we assume income will be zero in retirement, the preferred consumption bundle x,y incurs some degree of saving throughout the working-age period in order to be able to pay for consumption in the retirement period.

Also, we should note that working-age consumption could be raised beyond an amount that the person's income can afford if he/she were to borrow money rather than save it. That would, of course, not be possible to maintain indefinitely, and the longer that it is maintained the more that future consumption must be sacrificed.

We should also consider the impact that a different rate of interest will have on the person's preferred tradeoff between current and future consumption, and this is illustrated in the graph below.

The interest rate is an important determinant of saving/borrowing because it represents the price of loanable funds. A higher interest rate ought to encourage more saving, because any given amount of saving will grow at an accelerated rate and therefore allow extra consumption in future. The long-term effect of compound interest is powerful, and in the graph above this is represented by a shift from BL (budget line) to the much steeper BL'

A higher interest rate also makes a small reduction in the maximum amount of affordable consumption in the first period, because the higher interest rate increases the cost of borrowing.

For our consumer, the higher interest rate adds to the future value of saving, and therefore entices more of it. This is represented in the graph by the reduction in working-age consumption from x to x'. Retirement consumption increases greatly from y to y' as a result of the extra saving and higher interest rate. Overall utility is higher after the interest rate rise because our consumer is a saver. If the consumer was a borrower, utility would decrease because of the increased cost of borrowing.

As a final note regarding the intertemporal budget constraint, you should be aware that there may be some confusion arising as to what is meant by saving and consumption. If a consumer purchases a house, and borrows money to do it, you may be surprised to read that this is actually a form of saving. The important point here is to think of the consumption as it occurs rather than the immediate expenditure incurred.

When we buy a house, we are purchasing something that will provide us with shelter on an ongoing basis. This is not the same as consuming a donut, because once eaten a donut offers no future consumption. Cars, washing machines and other 'durable goods' do confer a future stream of services, but they are depreciating assets that are unlikely to survive into retirement. A house is a form of investment because it yields a future stream of shelter, and its value will usually increase over a lifetime as economic growth continues.

Sources:

• E. Sims - Intermediate Macroeconomics: Consumption (PDF)

Related Pages:

• The Budget Line & Budget Constraint
• Indifference Curves
• Utility Function
• Permanent Income Hypothesis 
• Consumer Behavior

ShareFacebookXPinterestTumblrRedditWhatsApp