Minimum Efficient Scale Explained (with Examples & Graph)

Questions about the minimum efficient scale of production arise for the executives of any firm when considering its long term competitive strategy. This is because long term survival will almost certainly require that the firm operates at, or close to, the lowest point on its long term average cost curve.

The minimum efficient scale relates to a point on that curve at which the economies of scale are first achieved i.e., the lowest amount of production that allows the firm to minimize its long run average costs of production. Clearly, the scale of production necessary to achieve these efficiencies will be very different depending on the nature of the industry, and I have discussed this in some depth in my article about the Economies of Scale.

In this article I will not discuss different industries, but I will go deeper into the practical meaning of the concept of a minimum efficient scale, because it does have some implications for the shape of the cost curves used in the standard textbooks and how they relate to outcomes in the real world.

I will start with another look at the textbook cost curves used for analyzing a firm's long term costs, so it's important to understand how these curves relate to each other, their shape and so on. For a refresher on that, and in particular on the relationship between LRAC and LRMC, refer to my article at:

• The Short Run & Long Run Average Cost Curve (SRAC & LRAC)

Minimum Efficient Scale Graph

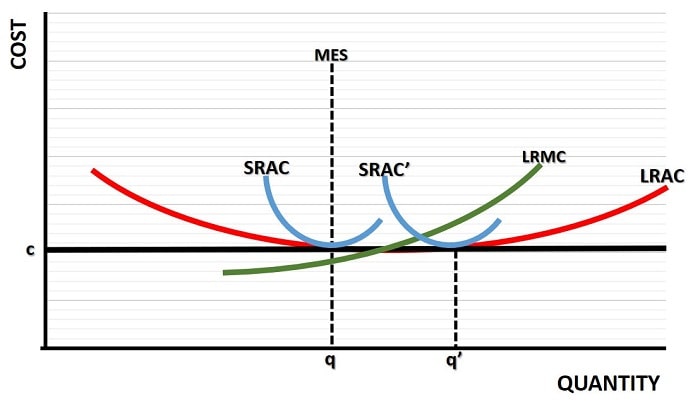
The key point to understand with the concept of a minimum efficient scale is that some portion of the LRAC must be flat, or close to flat. Only in this scenario is it possible for a range of different quantities of production to be consistent with optimal efficiencies of scale. This is illustrated in the graph below.

Minimum Efficient Scale Formula

The minimum efficient scale occurs at the lowest amount of production at which there are no further significant long run average cost reductions available from increasing output. If we were to try to express this in a formula, it would look something like:

MES occurs at the lowest q for which LRMC ≈ LRAC

Reflecting on the graph above, at first glance it may appear that the LRMC curve does not pass through the LRAC curve at a quantity close to the minimum efficient scale (MES). However, if you look again you will see that for all quantities between q and q' (the minimum and maximum efficient scale points) the LRAC is more or less equal at c. This must mean that the LRMC is almost equal to c throughout that production range. 

This does raise some immediate practical difficulties with the analysis given in the standard economics textbooks, which treat this subject as though any cost difference is significant, and students of economics should be aware of that. However, the models in those books are just theoretical abstracts used to illustrate a point.

For the concept of a minimum efficient scale to exist at all, there has to be a range of different output quantities over which there is more or less equal efficiency. In other words, while the textbooks assume that there is a range of output over which the LRAC curve is perfectly flat and costs are exactly equal, in reality it is technically impossible for those costs to be exactly equal over any production range. There will always be one particular quantity of output that has the absolute lowest average cost.

What matters here is that there is an 'almost' flat section of the LRAC curve over which any difference in the average cost of production is of no concern. Only in this sense is it possible for there to be a minimum efficient scale in the real world, and a range of output quantities that are more or less equally efficient. There will be some slight differences in LRMC over that range, but they are small enough that they fall within a margin of error when entrepreneurs try to estimate their costs of production.

Minimum Efficient Scale Example

An example of how firms use estimates of their MES is given in the PDF link below, and it relates to the preferred scale of container terminals in international shipping. In essence, the example given shows how firms in this particular industry often prefer to operate at a scale significantly different to that predicted by the standard economic model described above, and the primary reasons for that come down to market structure and available resources.

How Market Structure & Resources Affect Minimum Efficient Output

The following six main points help to explain the most important aspects of the global container terminals industry. It is an industry where the port management duties fall to the 'port authorities', who then lease out individual port container terminals to 'operators' who load and unload container ships.

The issue under examination relates to the lack of competitive forces in both the selection process of operators, and the efficient scale of terminals i.e., whether they are too small or too large to benefit from optimal efficiencies of scale. This will determine whether or not the industry operates at or around the MES.

• As always, there are practical difficulties in accurately estimating the MES for international container terminals. Many different methodologies are used in various locations around the world, and this makes uniform comparisons difficult.
• Competition is geographically segmented, which restricts the supply of container terminals because markets are smaller in some countries than others. The implication is that local monopolies exist and competitive forces are limited.
• There are some geographical locations and local markets that can only support smaller ports and terminals, meaning that terminal operators will not have access to some of the best cost saving resources, technologies, and infrastructure. Highly automated yard equipment like dual trolley cranes, for example, are only feasible in large terminals.
• Advances in technology may allow for greater economies of scale and therefore shift the MES to a higher rate of production. However, existing terminals may not be able to accommodate that new technology. In other words, existing port terminals may have to operate below MES for an extended period of time due to the 'sunk costs' that have already been invested into them.
• There are only a small number of buyers i.e., potential terminal operators, meaning that the port authority may have some difficulty ascertaining the highest competitive price that any potential operator is prepared to pay. For this reason some port authorities may prefer to opt for smaller terminals in order to generate a more competitive bidding process from a larger number of potential container terminal operators. However, those smaller terminals may not have the capacity to achieve a minimum efficient scale of production.
• If the port authorities develop terminals according to the specifications of potential terminal operators, those operators may wish for overly large terminals in order to create a local monopoly. That would tend to result in a terminal that operates above the MES with diseconomies of scale. 

The significant barriers to a fully competitive outcome in the container terminals industry, as explained by the six key points above, are enough to prevent firms from operating at the MES. Instead they operate at a 'preferred scale' that at times may be inefficient, i.e. lower than the minimum efficient scale or higher than the maximum efficient scale. 

Sources:

• E. N. Kaselimi Et al. - MES & preferred scale of container terminals (PDF)

Related Pages:

• The Long Run Average Cost Curve
• Economies of Scale
• Diseconomies of Scale
• Economies of Scope
• The Costs of Production
• The Production Possibilities Curve

ShareFacebookXPinterestTumblrRedditWhatsApp