The Production Function in Economics

The production function in economics helps us to understand how firms decide to organize various combinations of inputs into their most efficient uses so that they can create an optimal amount of goods and services to be sold on the market. Competitive forces in the market will favor the firms that minimize costs, and a production function describes a set of technically efficient production techniques.

The purpose of production functions, for economists, is to build up a better understanding of supply for both firms and markets. For simplicity, it is standard practice to limit our production techniques to various combinations of capital and labor. There are, of course, other factors of production that firms use but it would needlessly complicate the analysis to include them all. In its simplest form, a production function can be expressed as a formula:

q = F(K,L)

In words, this means that the quantity of output produced is a function of capital and labor. In the analysis that follows, keep in mind that inputs (and outputs) are flow concepts, so think of them as so much capital and labor per year to produce so much output per year.

Also keep in mind that we assume all other things are held constant i.e., technology does not advance over the period. Firms will select their preferred amounts of capital and labor from all possible combinations that can efficiently produce their target levels of output. This is an important concept i.e., that both capital intensive combinations and labor intensive combinations may be feasible, and different firms may prefer different combinations.

Special Case Production Functions

Before continuing on to general principles about production functions in the short-run and long-run, there are two special case functions that readers should be aware of as they are popular in the textbooks and exam papers. They both represent extreme cases, but they still have relevance in a number of real-world industries.  

The Leontief Production Function

The Leontief production function, also called the fixed proportions production function, describes a situation where there is no flexibility in the use of capital and labor in the production process i.e., they have to be used in specific fixed proportions to one another.

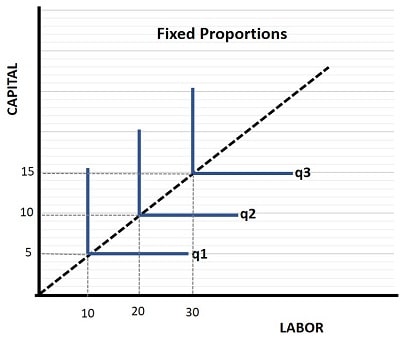
Each L-shaped isoquant in the graph represents a given quantity of output. A firm in this industry will always choose an input combination that intercepts the dashed line.

Whatever that proportion is, an additional input of capital (or labor) cannot increase production at all, unless it also comes with an additional proportional increase in labor (or capital). This is illustrated in the graph above with L-shaped isoquants.

There are many examples of the Leontief production function, and the most common relate to machinery that can only be operated by specific numbers of workers.

A computer programmer (labor) and a computer (capital) must be used in a 1-2-1 combination, because two or more programmers cannot work the same computer at the same time. Obviously there are exceptions where several programmers might work different shifts and use the same computer at different times of day, but that would just change the fixed proportion of labor to capital, the principle does not change.

Similarly, an aircrew (labor) and an airliner (capital) must be used in more or less fixed proportions to transport the same number of passengers. Adding another airliner without another crew will not increase the number of passengers transported.

The Perfect Substitutes Production Function

The second special case arises at the opposite extreme to Leontief production function where capital and labor can be used interchangeably with no loss of output. This is known as the 'Perfect Substitutes production function', and the graph below illustrates it.

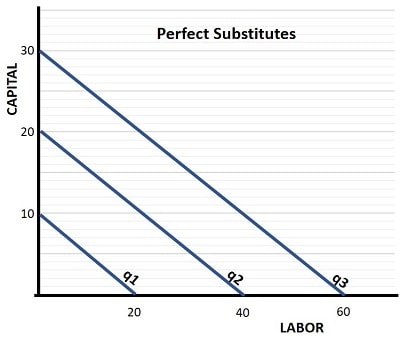
The linear isoquants in this graph indicate that a given quantity of production can be created by either input (capital or labor), or any combination of the two. Firms can therefore choose any input combination along each linear isoquant that they prefer, without impacting output. 

Examples of the perfect-substitutes production function are also many, because many simple products can be provided either by a machine or a worker. The important point to remember here is that we are not accounting for cost here, it will almost certainly be cost-effective to employ a specific proportion of capital and labor, but production functions only tell us what quantities of output can be produced with what combinations of inputs.

A car assembly plant may operate a production line with a certain amount of advanced robotics, or it may employ a certain amount of skilled workers. Both factors of production, labor and capital, can be substituted for each other in the long-run, but in the short-run labor is more flexible.

Of course, in the long-run the most cost-efficient method will be favored, but in the short-run a firm's advanced capital equipment is relatively fixed.

The Short-Run Production Function

As with other concepts in economics, the standard treatment of the short-run and the long-run applies, meaning that there is a significant time factor involved in a typical firm's ability to adjust all its preferred amounts of inputs (capital and labor). How long that is depends on the individual firm and the industry in which it operates.

For example, a typical offshore oil and gas firm will need many years to invest in new capital to develop a new oil rig, and that's true even after all the exploratory work is completed and a new potential drilling site is located. At the other extreme, a fruit seller at a local market stall is able to purchase/rent additional capital e.g., a van/truck, computer accounting software, a cash till etc, just as quickly as he/she can recruit more workers.

Most firms, however, do face a significant time delay before all factors of production can be adjusted, and it is standard practice in economics to assume that capital takes more time to adjust. This being the case, since our production functions only consider capital and labor, the short-run production function occurs over the time period where capital is a fixed input and labor is a variable input.

To understand the economics behind production with only one variable input, have a look at my article about:

• Marginal Product, Average Product & Total Product

The Long-Run Production Function

Having understood the short-run, it should be obvious that the long-run production function applies to the situation where all inputs in the production process have time to be adjusted. In this case, the analysis becomes slightly more complicated, but nothing too daunting.

The Cobb-Douglas Production Function

Special mention needs to be given to the Cobb-Douglas Production Function, which is easily the most well known long-run production function.

It takes the form F(K,L) = AKᶿLᵝ (where ᶿ and ᵝ are positive numbers).

Depending on whether ᶿ and ᵝ sum to a number less that one, equal to one, or greater than one, this function will apply to an industry with decreasing, constant, or increasing returns to scale.

Sources:

• The Production Function (PDF)

Related Pages:

• Marginal Rate of Transformation
• Isoquants and the Isoquant Map
• Marginal Rate of Technical Substitution
• The Short-Run & Long-Run Average Cost Curve
• The Law of Diminishing Returns
• The Production Possibilities Curve

ShareFacebookXPinterestTumblrRedditWhatsApp