Steve Bain

Understanding Marginal Revenue in Economics

Marginal revenue, in economics, is the term that applies to the additional income that a firm earns from selling one more unit of a product or service. That might not sound to impressive but it packs a lot more punch than you might think. There’s a common adage about economics that everything happens at the margin, and you’ll get a good idea of why that is true from this article.

By understanding marginal revenue, businesses can make more informed decisions regarding production levels, pricing strategies, and resource allocation, ultimately leading to enhanced profitability.

Marginal revenue is closely linked to the law of diminishing returns, which states that as more units of a good or service are produced and sold, the additional revenue generated from each successive unit will eventually decrease. This phenomenon occurs because, in most cases, businesses have to lower prices to sell additional units, especially in competitive markets. Marginal revenue, when used in conjunction with marginal cost, helps businesses to identify the best combination of price and output levels.

In economic theory, marginal revenue is often depicted graphically alongside marginal cost, which is the cost of producing one additional unit. The point where these two curves intersect is known as the profit-maximizing output level. If output was lower than this level, the marginal revenue gained from selling more output would be greater than the marginal cost of producing that output, and vice-versa if output was above the profit-maximizing level.

Graphs of the Marginal Revenue Curve

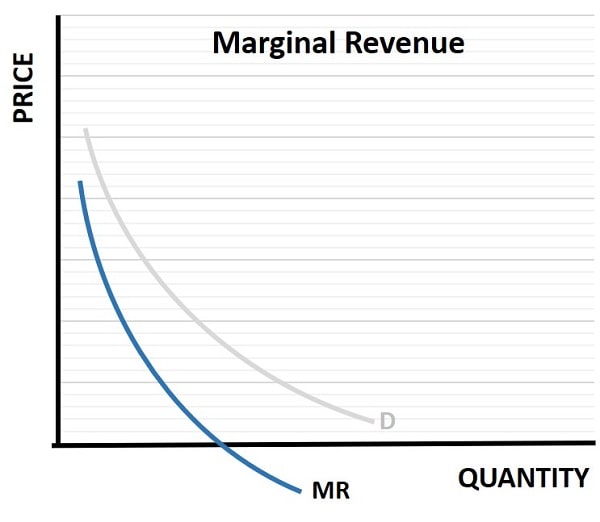
In the graph of the marginal revenue curve below, I have illustrated how marginal revenue varies with demand for a monopolist. In this case, the marginal revenue curve is lower than the demand curve, and steeper. The reason for this is because, in order to sell more of its product, it must lower the market price for all its goods, not just the next good.

The implication is that the marginal revenue for the monopolist is equal to the additional revenue gained from an additional sale minus the revenue lost from all previous sales that had been sold at a higher price. This being the case, a monopolist can even experience negative marginal revenue at relatively low levels of output compared to a competitive industry.

Marginal Revenue Curve Graph

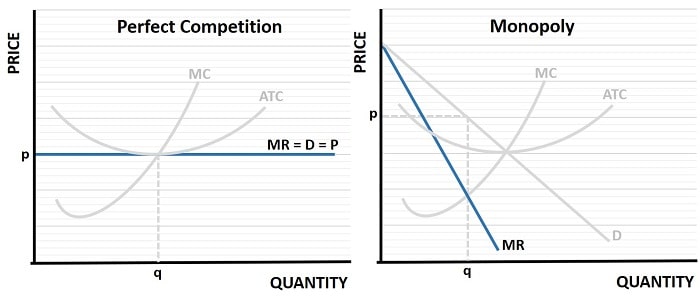
This is illustrated in the graph below which shows optimal price and output combinations for a competitive industry and a monopoly. As can be seen on the left-side of the graph, the marginal revenue curve for a firm in a competitive industry is horizontal, and equal its demand curve and price line. Competitive firms are price-takers, so their marginal revenue is equal to the fixed industry price. You can see from the graph that a monopoly will always optimize its profits by restricting output and charging a higher price than would occur in a perfectly competitive industry.

In both market structures, note that profits are optimized where the marginal revenue curve (MR) crosses the marginal cost curve (MC).

Marginal Revenue and Market Structure

I should point out here that these market structures are not complete, and the marginal revenue curve can take on some other characteristics under oligopoly. However, for more information on the market structures presented above, and related cost curves, have a look at my articles about:

How Marginal Revenue Affects Investment

Investment decisions are another critical area where marginal revenue exerts its influence. Businesses often face choices about whether to invest in new projects, expand production capacity, or enter new markets. Marginal revenue analysis helps companies evaluate the potential returns on these investments by comparing the additional revenue generated with the associated costs.

This enables businesses to make informed decisions that optimize their investment portfolios and drive sustainable growth. In essence, marginal revenue serves as a compass that guides businesses toward profitable and strategic choices across various operational domains.

Marginal Revenue vs Average Revenue

Average revenue refers to the total revenue earned by a firm divided by the number of units sold. It represents the revenue earned per unit of output. In contrast, marginal revenue is, as already explained, the additional revenue generated from selling one more unit of a product or service.

The relationship between marginal revenue and average revenue has significant implications for pricing and production strategies. In markets characterized by perfect competition, average revenue and marginal revenue are typically equal, this again because firms are price-takers and cannot influence market prices.

However, in imperfectly competitive markets, such as monopolies or oligopolies, marginal revenue is usually lower than average revenue due to the downward-sloping demand curve. This means that firms must lower prices to sell additional units, leading to a decline in marginal revenue.

Another important distinction is that average revenue remains relatively stable across different output levels, while marginal revenue can fluctuate significantly. This variability makes marginal revenue a more sensitive and precise indicator for optimizing production and pricing decisions.

How to Calculate Marginal Revenue

Calculating marginal involves a few straightforward steps that can be applied to various scenarios, from assessing new product launches to evaluating pricing strategies. The first step in calculating marginal revenue is to determine the total revenue at different output levels. Total revenue is calculated by multiplying the price per unit by the quantity of units sold.

For example, if a company sells 100 units of a product at $10 each, the total revenue is $1,000. Similarly, if the company sells 101 units at the same price, the total revenue increases to $1,010. By comparing these total revenue figures, businesses can assess the impact of changes in sales volume on overall revenue.

The next step involves calculating the change in total revenue resulting from a one-unit increase in sales. This is done by subtracting the total revenue at the initial output level from the total revenue at the new output level. Using the previous example, the change in total revenue is $1,010 - $1,000 = $10. This figure represents the additional revenue generated from selling one more unit of the product.

Finally, the marginal revenue is calculated by dividing the change in total revenue by the change in quantity sold. In the example above, the change in quantity sold is 1 unit, so the marginal revenue is $10 / 1 = $10. This means that the additional revenue generated from selling one more unit is $10. By repeating this process for different output levels, businesses can track how marginal revenue changes with varying sales volumes and make informed decisions accordingly.

Marginal Revenue Formula

If it is not possible to compile information in the way described above, economists can use mathematical techniques to calculate marginal revenue. In perfect competition this is not necessary since MR = P, and P (the price) can easily be observed. In non-competitive markets it is more complicated, and calculus becomes necessary. Even with calculus we still need to have an equation that expresses price as a function of quantity:

MR = d(TR)/dQ

Where: TR = P(Q) x Q and P(Q) is price as a function of quantity.

An alternative function, if we know the price elasticity of demand, is:

MR = P(1 + 1/Ed)

Where: P is price, and Ed is the price elasticity of demand.

The Role of Marginal Revenue in Pricing Strategies

One of the primary ways in which marginal revenue informs pricing strategies is through its impact on price elasticity of demand. Price elasticity of demand measures how sensitive consumers are to changes in price. When demand is elastic, a small change in price leads to a significant change in quantity demanded. Conversely, when demand is inelastic, changes in price have a minimal effect on quantity demanded.

Marginal revenue also plays a crucial role in dynamic pricing strategies, where prices are adjusted in real-time based on market conditions, demand fluctuations, and competitive dynamics. In industries such as hospitality, airlines, and e-commerce, dynamic pricing is a common practice to maximize revenue.

Another important consideration is the role of marginal revenue in price discrimination strategies, where businesses charge different prices to different segments of customers based on their willingness to pay. By analyzing marginal revenue across different customer segments, businesses can identify opportunities for price differentiation that enhance profitability. For example, offering discounts to price-sensitive customers while maintaining higher prices for less price-sensitive segments can maximize revenue without alienating any customer groups.

Real-World Examples of Marginal Revenue in Action

Examining real-world examples of marginal revenue in action provides valuable insights into how businesses leverage this concept to drive profitability and strategic decision-making.

  • One notable example is the airline industry, where dynamic pricing strategies are heavily influenced by marginal revenue analysis. Airlines utilize sophisticated revenue management systems to adjust ticket prices in real-time based on factors such as demand fluctuations, booking patterns, and competitive actions. By closely monitoring marginal revenue, airlines can identify the optimal price points that maximize revenue from each flight.
  • The technology industry also provides compelling examples of marginal revenue in action. Companies like Apple and Microsoft often use price discrimination strategies to maximize revenue from different customer segments. By offering multiple product versions with varying features and price points, these companies can capture additional marginal revenue from customers with different willingness to pay.

FAQs

How does marginal revenue behave in a kinked demand curve model of oligopoly?

In a kinked demand curve model, marginal revenue has a discontinuity — a vertical gap at the kink. This reflects different elasticities above and below the current price. Firms expect rivals to match price decreases but not increases, which causes marginal revenue to jump abruptly and leads to price rigidity in oligopolistic markets.

Can marginal revenue ever be negative, and what does that indicate?

Yes, marginal revenue can be negative, particularly in monopolistic markets. This occurs when the loss in revenue from lowering the price on all previous units outweighs the gain from selling one additional unit. Negative MR signals that increasing output actually reduces total revenue, indicating overproduction.

What is the relationship between marginal revenue and total revenue curves?

Marginal revenue is the slope of the total revenue (TR) curve. When MR is positive, TR is increasing; when MR is zero, TR is at its maximum; and when MR is negative, TR is decreasing. This relationship helps firms understand how output decisions affect overall earnings.

What role does marginal revenue play in determining market power?

Firms with significant market power can influence prices and typically have marginal revenue curves that diverge from demand curves. The greater the gap between price and marginal revenue, the more pricing power the firm has — a key indicator of monopoly or oligopoly behavior.

How does marginal revenue interact with consumer surplus and deadweight loss?

Marginal revenue pricing often leads to output levels below what a perfectly competitive market would produce. This creates deadweight loss — missed opportunities for mutually beneficial trades — and reduces consumer surplus. Understanding MR helps identify the extent of inefficiency in monopoly or oligopoly markets.

How does marginal revenue relate to pricing in subscription-based business models?

Subscription models benefit from predictable revenue, but marginal revenue still matters — especially when upselling, cross-selling, or reducing churn. Firms analyze MR from new subscribers versus existing ones to fine-tune acquisition and retention efforts and maximize customer lifetime value.

Conclusion

Understanding and leveraging marginal revenue is crucial for businesses seeking to unlock their profit potential and achieve sustainable growth. Marginal revenue is a powerful tool that informs strategic decisions across various facets of business operations. From optimizing production levels and pricing strategies to navigating competitive dynamics and making informed investment choices, marginal revenue plays a central role in driving profitability and competitive advantage.

By calculating marginal revenue accurately and analyzing its relationship with marginal cost, companies can identify the profit-maximizing output level and avoid the pitfalls of overproduction or underproduction. Additionally, understanding the impact of market structure on marginal revenue enables businesses to navigate competitive landscapes and develop strategies that align with their market positioning.

Furthermore, real-world examples from industries such as airlines and technology demonstrate the practical applications of marginal revenue analysis in driving revenue growth.

Related Pages:

Show / Hide