The Saving Function in Economics (Formula & Graph)

The saving function in economics arises from John Maynard Keynes' work on the consumption function, but it has limited practical use in the real world because it can only be used in simple economic models where we exclude government and foreign trade. For a fuller explanation of Keynes' model, see my main article at:

• The Keynesian Consumption Function

When we make these exclusions we limit national income to a combination of consumption expenditure and investment expenditure, and investment can only be funded by savings. This means we can state that:

• Y = C + I
• S = I

In words, national income (Y) is equal to consumption expenditure (C) plus Investment expenditure (I), and saving (S) is equal to investment.

Intuitively we can see that this must be true, because in this simple model saving means non-consumption. Income can be either saved or consumed, and only that which is saved can fund investment.

You can probably begin to understand why we have to exclude government and foreign trade from the saving function formula, because either of those two can provide the funds for investment irrespective of saving, and that would break the S = I requirement.

The Saving Function Graph

The top part of the graph below is taken from my article about the Consumption Function Formula.

On that page I explained how the consumption in this simple economy is formulated by the equation C = A = cY and that the slope of that function is equal to c. This is illustrated by the dark blue line in the saving function graph below.

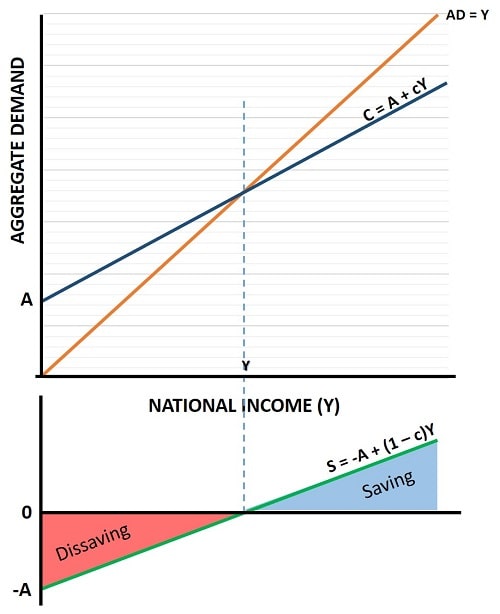
Now, since c represent the slope of the line, and since it is a measure of the proportion of national income that is consumed, it follows that whatever remains must be savings. Since consumption and saving must equal 1 i.e., the marginal propensity to consume (c) and the marginal propensity to save (1 - c) must add up to 100 percent of income, it follows that the slope of the saving function must be equal to 1 - c as illustrated by the green line in the bottom half of the graph.

Also note that the autonomous consumption A that occurs when national income is zero (see my article about the consumption function formula for an explanation of this) can be illustrated by the saving function as negative saving, or dissaving, of -A.

Plotting the saving function below the consumption function illustrates all levels of national income for which there are resulting negative or positive amounts of saving. Naturally, since saving equals investment in this simple model, the same formula can be described as an investment function.

The Saving Function Formula

As explained above, the saving function formula can be written as:

S = -A + (1 - c)Y

Now, you may wonder what would happen if firms did not wish to invest the same amount of money that savers wished to save. Well, in this simple model without government interference, interest rates would be allowed to settle at a rate that clears the market, just as prices clear any other market.

If saving is higher than desired investment, the interest rate would fall until saving was discouraged and investment borrowing was encouraged enough to reach equilibrium.

In the real world, of course, interest rates are not allowed to settle at a market rate and so the link between saving and investment is broken. As you can read on my main page about the consumption function, investment is actually treated as being autonomous of income, and being chiefly dependent of business confidence with regard to anticipated future demand for their products.

This is, of course, highly volatile in nature and forms one of the primary explanations of the business cycle in Keynes' General Theory of Employment Interest and Money. In that work he makes the case for government intervention in the economy, and the use of government spending and monetary policy (interest rate manipulation) to manage the boom bust cycle. Whether that makes sense or not is highly debatable, and it certainly flies against everything the Austrian School of Economics would recommend.

Related Pages:

• Consumption Function Shifts
• Determinants of Consumption
• The Keynesian Consumption Function

ShareFacebookXPinterestTumblrRedditWhatsApp