What is Productive Efficiency in Economics?

Productive efficiency refers to the efficient use of the inputs used to create goods & services i.e., land, labor, capital, and enterprise. For simplicity, the models that economists use to explain the efficient use of inputs tend to focus only on labor and capital. Similarly, we focus on production of only two alternative goods, cheese and biscuits in the examples below.

These simplifications may seem to be unrealistic, but the ideas explained are unaffected. All economic models are gross simplifications of real-world scenarios, but they still work to explain basic principles.

Before continuing I should point out that the models used here are static short-term models where the level of technology and innovation is held constant. Efficiency over the long-term is dealt with in my article about Dynamic Efficiency.

As an additional note, I caution you to be aware that there are many established economics websites that treat the following matter in serious error. They use standard excess demand or excess supply analysis, among others, as per typical partial equilibrium models, but the correct analysis here requires general equilibrium models.

That's an important point for any student to be aware of, and if in any doubt you should always refer to a course-approved textbook.

The Production Possibilities Curve

The diagram below, taken from my article about the Production Possibilities Curve, illustrates a frontier of maximum possible combinations of biscuits and cheese. Points A and B, which lie on the frontier are technically efficient combinations of goods given the inputs that are available to our economy at a given point in time.

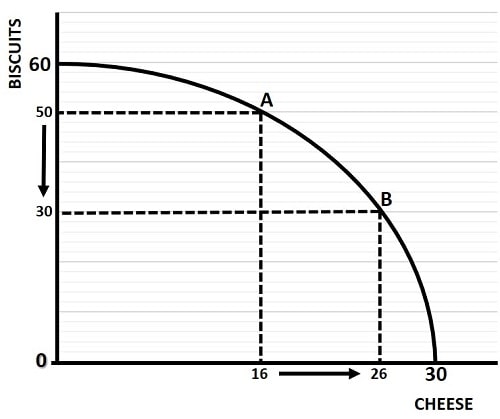The Production Possibilities Curve/Frontier

Any points below the frontier are inefficient since it is possible to increase production, and efficiency requires that we satisfy the basic rule of economics that more is better. Points above the frontier are impossible since we do not, in the short-term, have sufficient resource inputs in order to produce beyond our current frontier.

Technical Efficiency

A particular combination of all available inputs into the production process is called ‘technically efficient’ if it leads to a situation where the production of neither good can be increased without necessarily sacrificing some production of the other good. In other words, this occurs where any given combination of goods is being produced at the optimum rate possible, and at the lowest cost possible.

Many economists use the terms ‘productive efficiency and ‘technical efficiency’ interchangeably, but there are some who differentiate the two terms.

• Productive Efficiency – is sometimes used when we hold the total production of our two goods as fixed and then seek the most efficient use of inputs to achieve that production.
• Technical Efficiency – looks at it from the other direction and holds the allocation of inputs as fixed while seeking for the most efficient combinations of goods to produce.

Productive efficiency occurs where the relative cost of using an extra unit of labor is equal to the relative cost of using an extra unit of capital given the resulting increases in output.

For example, if an extra unit of labor costs $10 and an extra unit of capital costs $20, firms will use labor and capital until the marginal product of both is equalized. This would happen where the last unit of capital yields extra output at a rate twice that of labor, because capital costs twice as much to use.

In words we say that the marginal product of labor divided by the marginal product of capital is equal to the wage rate divided by the cost of capital (i.e., the interest rate). We write this in the form:

MP(L)/MP(K) = w/r

In my article about the Marginal Rate of Technical Substitution (MRTS), I showed that MP(L)/MP(K) = MRTS(LK), which can be substituted in the equation above so that:

MRTS(LK) = w/r

In other words, for productive efficiency to be reached, the marginal rate of technical substitution between labor and capital is equal to the wage rate divided by the interest rate. For more clarity on this, click the MRTS link above.

The Marginal Rate of Transformation and Substitution

So far, we have focused more or less exclusively on the producers' ability to supply various combinations of products and the costs of doing so. This is fine but we also need to consider the economics involved with consumer preferences i.e. what bundles of goods the market actually has a demand for.

In the diagram below I have illustrated how these two concepts combine to achieve the greatest value for producers and consumers. The blue indifference curve illustrates various bundles of goods that consumers derive equal 'utility' from i.e. they provide equally satisfying combinations.

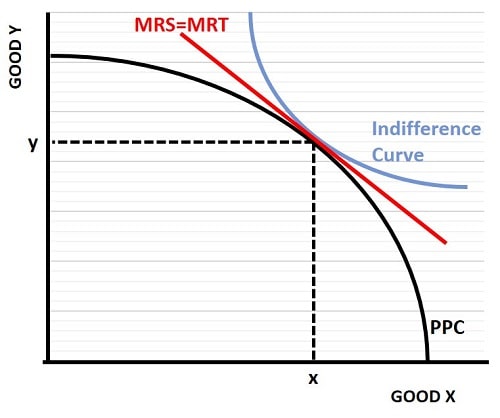The optimal marginal rate of transformation and substitution

Only at the point where the indifference curve touches the production possibilities curve (PPC) is it possible to maximize both producer output and consumer satisfaction. That point occurs with a bundle of x,y.

At this point, there is an equal marginal rate of substitution (MRS) and an equal marginal rate of transformation (MRT). The marginal rate has equal slope for both the transformation of producing one good for another, and for substituting a preferred amount of one good for an equally preferred amount of the other.

In a closed economy this represents maximum efficiency and an optimal level of consumption, but it is possible to gain even greater levels of consumption via the gains from trading with other countries. The economics here is a little more complicated but easily grasped once the reader has understood the basic model above.

Conclusion

In conclusion I will start by reiterating what I wrote at the beginning; too many online influencers treat the topic of productive efficiency, and other economic efficiency models, as though they belong to the partial equilibrium scope of particular firms and industries. This is not the correct footpath to follow.

These efficiency models refer to efficiency in the whole economy, not just a part of it.

General equilibrium analysis is the correct framework for this area of economics. Some websites confuse these models with efficiencies resulting from social outcomes being different to private free-market outcomes. This again is incorrect, such concerns belong within a particular area of market failure economics known as ‘externalities’.

Productive efficiency and allocative efficiency models make the simplifying assumption that the economy is operating in perfect competition. This is just to make the analysis clear and bring important concepts forward, it is not meant to represent the real world – no model can.

Where particular inefficiencies arise, and there are many, they are analyzed with specific models of their own. Interested readers can look up my article on market failure (and associated articles) for more information about that.

Sources:

• F. Deng & G. K. Leonard – Allocative and Productive Efficiency (PDF)

Related Pages:

• Allocative Efficiency
• X-Efficiency
• Pareto Efficiency
• Economic Efficiency
• Market Failure

ShareFacebookXPinterestTumblrRedditWhatsApp