The Price Consumption Curve with price changes

The price consumption curve adds extra depth to the theory of consumer behavior with respect to movements in the prices of goods and services. I have previously written about utility maximization given budget constraints (see links below) but the price consumption curve takes us a little further and allows us to do a demand curve derivation.

Demand curves are, of course, fundamental to microeconomic analysis and it pays to understand the theory behind them. As always, we need to keep in mind the basic assumptions of consumer behavior in order to keep things in perspective, so click the link if you need a refresher.

I will, on this page, only be looking at how price movements affect demand. That means that all other variables, especially income, are held constant so that the effects of price changes can be seen without any distortions from other factors. This is standard practice in economics, and later models do build up the theory to provide a more complete picture of demand fluctuations in the real world when multiple factors may be influencing things.

As is often the case in economics, a graph is a useful starting point for illustrating the key points.

Price Consumption Curve Graph

In the price consumption curve graph below, I have again presented a situation where a consumer has a choice of only two goods on which to allocate a given budget i.e., cheese and biscuits. In this example the budget is set at $25 and the price consumption curve plots all combinations of cheese and biscuits that the consumer will choose when the price of cheese varies. The price of biscuits does not change, it is fixed at $1.00 per serving.

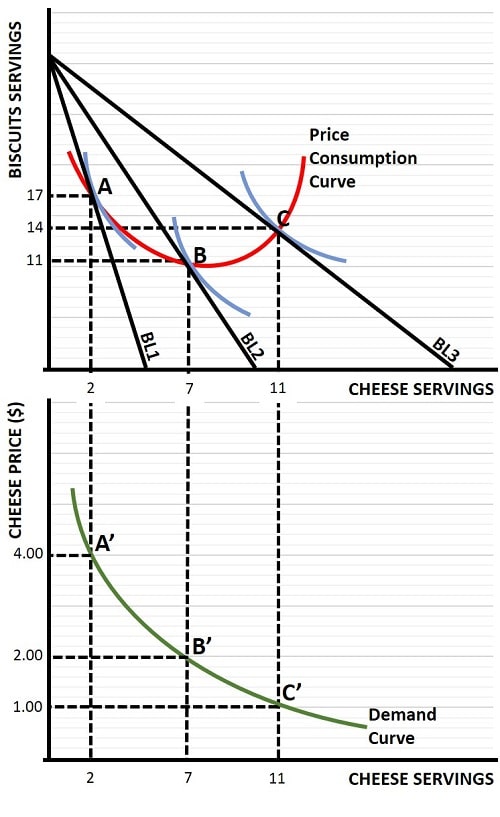
The resulting combinations of these two goods, illustrated by the price consumption curve, are chosen to maximize utility. We know this because, for each budget curve that results from each price of cheese, the corresponding highest possible indifference curve touches the budget line at the preferred consumption bundle.

Price consumption tradeoff with a fixed budget

In the top half of the graph above, the three blue indifference curves illustrate the optimal utility level for each of the three budget lines (BL1, BL2 & BL3). Those three budget lines result from three alternative prices for cheese i.e., $1.00 per serving, $2.00 per serving, and $4.00 per serving. We see that the budget lines extend further outwards on the horizontal axis at cheaper prices for cheese, because greater quantities become affordable given our $25 budget.

Starting with BL1, and a cheese price of $4.00 per serving, the highest achievable indifference curve touches BL1 at point A, with 2 servings of cheese and 17 servings of biscuits being the utility maximizing consumption bundle. Point A also denotes the first point that lies on the red price consumption curve.

Similarly, points B and C in the top half of the graph denote two more points that lie in the price consumption curve, and if we were to plot all such points for all possible cheese prices, we would map out the entire consumption curve.

An Upward Sloping PCC Example

Sticking with the top half of the graph above, you may have noticed that the red price consumption curve (PCC) has an upward sloping section. The reason for an upward sloping PCC is explained by the existence of an 'income effect' and a 'substitution effect' when the price of cheese changes. Both of these effects are always in operation, but which one is dominant depends on consumer preferences.

As we move from point A to Point B, the consumer reacts to the reduced cheese price (from $4.00 to £2.00) by preferring to purchase so much more cheese that part of his/her budget if substituted away from biscuits.

We can see that at the old price the $25 budget was allocated with $17 spent on biscuits (17 servings at $1.00 per serving) and $8 spent on cheese (2 servings at $4.00 per serving). At point B the budget is allocated as only $11 spent on biscuits and $14 spent on cheese (7 servings at $2.00 per serving). Since the consumer substituted some of his/her expenditure away from biscuits in order to get extra cheese servings after the price of cheese was reduced from $4 to $2 per serving, we conclude that the substitution effect was dominant.

Now, using the same logic, we can see that when the cheese price is further reduced from $2 to $1 per serving, the consumer allocates a larger portion of the budget to purchasing biscuits. Cheese consumption still increases from 7 servings to 11 servings, but expenditure on cheese falls from $14 (7 servings at $2 each) to only $11 (11 servings at $1 each). The increased spending on biscuits in consumption bundle C, compared to B, illustrates that the income effect of a reduced cheese price is dominant.

Demand Curve Derivation

The bottom half of the graph shows the individual demand curve that can be drawn according to the price movements and resulting consumption preferences for cheese servings. Note that the bottom half of the graph is only concerned with cheese servings and their prices, it is not concerned with biscuits since we have held the price of that good fixed.

Plotting the preferred price and quantity combinations for cheese gives us the simple downward sloping demand curve as illustrated, but consider also what this implies with reference to the marginal rate of substitution (MRS). In my article about the Budget Line I explained why, at the utility maximizing point, the slope of the MRS for normal goods is equal to the ratio of the price of one good compared to the other (with the one exception being a 'corner solution').

In the graph above the MRS of cheese for biscuits is given by the formula MRS = P(c)/P(b) which simply means that as the price of cheese P(c) gets lower, the MRS gets smaller. Now, since the demand curve shows all the utility maximizing points relative to price changes, it follows that the demand curve necessarily has a falling MRS as we move down it to lower and lower prices. In essence, the MRS of biscuits for cheese decreases as the cheese price decreases because of the increasing power of the income effect, i.e., because of the extra utility gained from increasing consumption of both goods, not just cheese alone.

The Price Consumption Curve & Income Consumption Curve

The consumption curve examined on this page has related to normal goods and associated price changes, but it is reasonable to wonder about other variables such as income. When income rises it will increase the budget available to the consumer and have direct consequences for consumption levels. The relevant consumption curve in this case becomes the income consumption curve, and in my article about the Engel Curve I have included full details of this, along with a look at consumption patterns for both normal and inferior goods at different levels of income.

Related Pages:

• The Budget Line & Budget Constraint
• The Indifference Curve
• Marginal Rate of Substitution
• Marginal Utility
• The Engel Curve & Income Consumption Curve

ShareFacebookXPinterestTumblrRedditWhatsApp