Revealed Preference Vs Stated Preferences

Revealed preference methods and stated preference methods are both techniques that businesses, economists, and other economic agents use to gain insights into the most valued combinations (or baskets) of goods and services that consumers desire.

This information is useful for obvious reasons - it helps firms to allocate their productive resources into the most economically efficient products i.e. the most profitable products.

However, there are significant difficulties involved in gathering this information, as well qualitative differences in the data depending on which of the two methods are used.

The revealed preference approach certainly provides more reliable data since it uses actual purchasing choices, but it is much more costly to obtain. Stated preferences on the other hand are much easier to obtain via simple consumer surveys, but the data is somewhat less reliable.

Revealed Preference Theory

Using revealed preference theory we can start to deduce certain properties that apply to any given indifference curve. I will assume here that the reader has a working knowledge of indifference curves but if that is not the case then I have written an article in this topic which you can access at:

• The Indifference Curve & Indifference Maps

There is a fairly serious difficulty with the practical use of revealed preference for estimating the location of indifference curves in that it requires quite a lot of information about the typical consumer's preferred basket of goods at differing prices and for different income levels, but that is not our problem here, here we simply assume that some of that information is known.

In the revealed preference graph below, we start at position (a) on the budget line BL1. Our task is to reveal the indifference curve that is tangential to the BL1 line at point (a). In order to do that we will need to know a number of other preferred consumption bundles when the two alternative goods considered are available at different prices, and when the consumer's income varies.

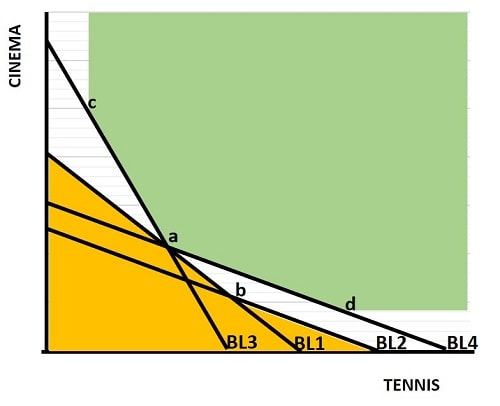
This requires that we have information about the preferred consumer bundle relating to different budget lines that pass through point (a) when the prices of the two alternative goods change. For simplicity, imagine that the two goods relate to two different leisure alternatives i.e. going to the cinema or playing tennis.

BL1 results when, for a given income, the prices of these two options are more or less even for a unit of consumption. Position (a) represents the optimal, or most preferred, consumption bundle in this scenario.

Now, imagine that the consumer's income falls so that less money is available to be spent on leisure activities. In this case we would need to illustrate a new, lower budget line. This is shown as BL2, and with the lower income level the optimal consumption bundle for our typical consumer is given at position (b).

What can we deduce so far? Well, given our assumptions about consumer preferences (as set out in my article about consumer behavior) we can confidently state that the consumer will have a preference for consumption bundle (a) over bundle (b) because position (b) also sits on the budget line BL1 and when the consumer has an option of choosing between (a) and (b) he/she chose (a). We can also deduce that compared to consumption bundle (a) all other points along or below BL1 are less desirable. Similarly, since bundle (b) is the preferred bundle at the lower income line BL2, we can assume that all other points along BL2 and below it are less desirable.

It follows from these deductions that all points in the orange shaded area in the revealed preference graph above must be less desirable than consumption bundle (a), and that the indifference curve tangential to BL1 at position (a) must therefore lie above the orange shaded part of the graph.

Next, let's again start at position (a) in the graph and this time hold income constant. Instead we'll consider what happens to the consumer's consumption bundle preferences when the prices of cinema tickets and tennis courts move in opposite directions. The BL3 line illustrates the attainable bundles of cinema tickets and tennis courts that can be bought/hired when cinema tickets are cheaper and tennis courts are more expensive (compared to BL1).

With the new prices, BL3 illustrates that the consumers consumption bundle preference occurs at position (c). Now, notice that BL3 passes through position (a) and is therefore available to the consumer. We can deduce therefore that consumption bundle (c) is preferred to bundle (a) and is therefore also preferred to all points in the orange shaded area.

We can also deduce that if (c) is better than (a) then all points along BL3 as we move away from (a) and towards (c) are also better than (a). We know this because the marginal rate of substitution is constant along this line, so moving along it from (a) to (c) gets increasingly better until we arrive at (c).

We also know that for any given point above or to the right of the budget line is preferred to points along that curve, since it yields more of at least one of the two goods under scrutiny. For more clarity, see my article about:

• The Budget Line & Budget Constraint

Now, BL4 illustrates that consumption bundle (d) is preferred when prices move in the opposite direction i.e. starting with BL1, cinema tickets get more expensive and tennis courts get cheaper to hire. BL4 also passes through point (a) and yet (d) is preferred to (a). Using the same logic as before, it follows that all points along the line BL4 between (a) and (d) are preferred to (a), and all points above that line are similarly preferred to (a).

Finally, putting all this together, compared to point (a), all points in the green shaded area must be preferred to point (a), while all points in the orange area are less preferred. It follows that the indifference curve that is tangential to point (a) and that sits on BL1 must pass through the un-shaded area of the graph. 

Revealed Preference Methods

A practical example of revealed preference is given by the graph below where, continuing with our cinema and tennis options, we show what happens when the Tennis court business adopts a membership scheme whereby our typical consumer gains extra utility from the resulting new pricing system.

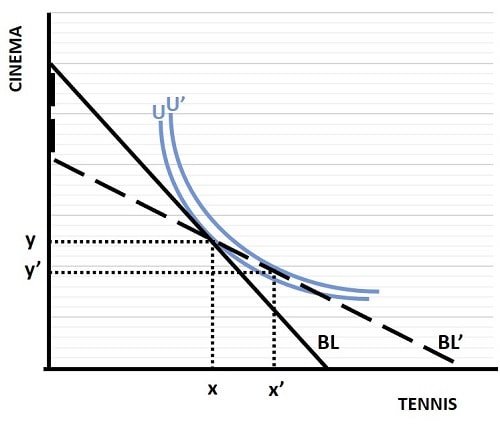
The original pricing scheme yields the budget line BL, but after a membership scheme is introduced by the Tennis court business (whereby a flat membership fee is introduced followed by a reduced cost for actual cinema tickets), the budget line shifts to the dashed BL' line.

The vertical part of the BL' line illustrates the membership fee that must be paid before any tennis courts can be hired. The flatter downward sloping part of the BL' line actually touches the horizontal axis at a higher quantity than the original BL line, meaning that if a customer where to spend his/her entire leisure budget on tennis, he/she would be able to enjoy an extra amount of tennis than before the new membership scheme was introduced.

For our representative consumer, the preferred choice is to move from a consumption bundle of x,y to x',y' meaning that consumption of cinema falls and tennis increases. The consumer gains extra utility from this as illustrated by the higher indifference curve U' compared to the original curve U. Note, however, that the membership scheme doesn't necessarily lead to a higher level of utility. If the consumer had responded to the new membership scheme by reducing the quantity of tennis played and instead favoring more cinema, the resulting utility curve would necessarily be lower than the original curve. 

Bounded Rationality Economics

Bounded rationality in economics is an important concept when it comes to our ideas about preferences. We assume rational behavior on the part of individuals when they make their choices about how to allocate their spending and consumption, but there are caveats. In particular, it is not necessary that a consumer obtains optimum 'utility' from a preferred consumption basket, it is only necessary that the consumer believes that his/her choices will optimize the utility gained at the time that he/she decides what to consume.

There are other caveats, but I won't repeat them here as I have already set them out on my page about consumer behavior where I list some assumptions about preferences. It is important to be aware of those assumptions in order to make sense of the models used here, and to be ready to answer all sorts of 'what if' questions that might arise.

I do, however, want to cover some well known axioms about revealed preference that are rooted in bounded rationality, and that relate to revealed preference theory as set out above:

Weak Axiom of Revealed Preference (WARP)

The weak axiom of revealed preference is demonstrated by the consumer's preference for consumption bundle (a) in the top graph. Bundle (b) was available to the consumer as it was also located on his/her original budget line BL1. So, the consumer has revealed their preference for (a) over (b), and the weak axiom of revealed preference states that with given preferences that consumer will never choose (b) over (a) at the existing prices.

Strong Axiom of Revealed Preference (SARP)

The strong axiom of revealed preference relates to 'transitivity' as discussed on my page about consumer behavior. In the graph at the top of the pages we indirectly revealed that consumption bundle (c) is preferred to bundle (b) because we show that (c) is preferred to (a) and we also showed that (a) is preferred to (b). This axiom denies the possibility of a sort of rock, scissors, paper relationship and insists that if the rock is preferred to the scissors, and the scissors are preferred to the paper, then the rock must also be preferred to the paper. Clearly this violates the well-known game, but in revealed preference we need this assumption to hold in order to maintain consistency.

Generalized Axiom of Revealed Preference (GARP)

The generalized axiom of revealed preference deals with situations in which a consumer may derive equal 'utility' (satisfaction) from two different bundles with a given income and fixed prices. This however, would violate our assumption that indifference curves are bowed (concave to the origin) since such an indifference curve can only touch a budget line at one distinct point. GARP therefore denies multiple equally preferred bundles since that would require a flat section of an indifference curve i.e. a section with an equal marginal rate of substitution, and this is inconsistent with our model.

Stated Preference Methods

As I mentioned in the page opener, stated preferences are easier to gather than revealed preferences since they can be built up from simple surveys rather than having to observe actual purchasing choices at various price points, but there is less reliability in this data.

That doesn't mean that stated preference data isn't useful, and it has been used extensively in marketing, transport economics, environmental economics and health economics in recent years. In some cases e.g., where new products are being introduced, it is not possible to use revealed preference modelling and so stated preference modelling has to be used instead.

It is also useful and practical to combine the two methods together, and careful planning to control for error variances between data sets does allow the use of stated choices to enrich traditional revealed preference analysis.

Sources:

• T. Demuynck & P. Hjertstrand - Revealed Preference (PDF)

Related Pages:

• The Utility Function
• Marginal Utility
• The Price Consumption Curve
• The Engel Curve

ShareFacebookXPinterestTumblrRedditWhatsApp