- Home
- Production Possibilities Curve
- User Cost of Capital

User
Cost of Capital Explained, (with Graph, Formula & Example)
The user cost of capital refers to the ongoing cost that a firm faces if it wishes to maintain a desired amount of capital stock. For simplicity, economists usually explain this in terms of the rental cost of capital since this is an ongoing cost, but the same principle applies to purchased capital.
If purchased, capital does not last forever and so its rate of depreciation must be taken into account. Similarly, when capital is purchased, a firm will have to use money to make the purchase, in which case there is an interest rate cost since borrowing money comes with an interest charge, and using retained profits comes with a loss of interest that could have been earned via an alternative investment to buying capital.
In the analysis below, I will illustrate how firms decide on their desired capital stock and then proceed to explain how to calculate the user cost of capital. I’ll explain the components of user cost, and I will present a simple formula that is often used to represent the user cost of capital.
The User
Cost of Capital Graph
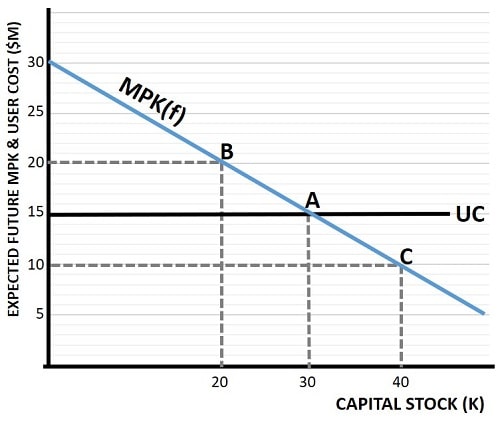
In the graph above, the expected future marginal product of capital (MPKf) and the user cost of that capital is presented, on the vertical axis, in terms of a dollar cost per year. I’ll assume that the representative firm here is a widget factory.
Example: What
is the firm's desired capital stock?
At point A on the graph, with a cost of $15m per year, the widget factory expects that the future marginal product of capital is equal to its user cost. On the horizontal axis it sees that this corresponds to a capital stock of 30 widget making machines. This is an equilibrium point which maximizes profits, and therefore the firm will have a desired capital stock of 30 machines.
If instead, if the firm was at point B on the graph, the firm expects that its MPKf is $20m per year while its user cost is only $15m. With MPKf higher than user cost, the firm could make extra profits by renting/buying more machines. At point C the opposite is true, the MPKf is below cost, and the firm should reduce its capital stock.
While the MPKf is downward sloping due to the law of diminishing returns, the UC line is flat because we assume that the firm is operating in a competitive market, meaning that it is a price taker. The firm cannot influence the selling price or rental rate of widget making machines, it simply takes the price as constant at $15m per machine in the example above.
How do you
calculate user cost of capital?
The graph above gives a simple illustration of how to calculate the user cost of capital, but it is more typical to set out the components of user costs and to present them as an equation of some sort. In the rest of the article, I assume that capital is bought rather than rented, as is usually the case in economics.
What are the
components of user costs?
The two components of user cost of capital are, as mentioned above, the depreciation rate of capital and the relevant real interest rate i.e., the rate paid on borrowed money (or the rate foregone on using retained profits) over and above the inflation rate.
The user
cost of capital formula
The user cost of capital is equal to interest plus economic depreciation and, since MPKf is equal to UC in equilibrium, this can be formulated as:
MPKf = UC = rPk + dPk = (r+d)Pk
In other words, if either the interest rate, the price of capital, or the rate of depreciation on capital falls, then the user cost of capital will fall and, ceteris paribus, firms will increase their desired capital stock.
Desired capital stock may also increase if the level of technology improves, meaning that the firm’s MPKf would rise higher in the graph above.
The tax-adjusted
user cost of capital
Finally, when taxes are charged on the firm’s profits, its MPK is effectively reduced. This means that the MPKf must be adjusted for that tax rate proportionately. This is done by dividing the equation above by 1 minus the tax rate(t):
MPKf/(1-t) = UC/(1-t) = (r+d)Pk/(1-t)
Conclusion: User
Cost & Desired Capital Stock
The user cost of capital reflects the total economic cost incurred by a firm when utilizing its capital assets in the production process. Comprising depreciation and interest as the main components, this metric aids in rational decision-making regarding the allocation and utilization of capital resources.
Firms assess the user cost in comparison to expected returns i.e., MPKf, to determine the profitability of utilizing capital goods. If the expected returns surpass the user cost, it becomes economically viable to employ extra capital stock in production.
In parallel, the concept of desired capital stock is crucial for firms seeking to optimize their production efficiency. Desired capital stock represents the ideal quantity of capital goods a firm aims to maintain for optimal productivity and profitability and, over time, firms strive to align their actual capital stock with the desired level.
Related Pages:
- The Isocost Line
- Cost Minimization
- The Marginal Rate of Technical Substitution
- Costs of Production
- The Production Possibilities Curve
About the Author
Steve Bain is an economics writer and analyst with a BSc in Economics and experience in regional economic development for UK local government agencies. He explains economic theory and policy through clear, accessible writing informed by both academic training and real-world work.
Read Steve’s full bio
Recent Articles
-
What Happens to House Prices in a Recession?
Jan 11, 26 03:13 AM
What happens to house prices in a recession? Learn how different recessions affect housing, why 2008 was unique, and how policy responses change home values. -
Does Government Spending Cause Inflation?
Jan 10, 26 06:01 AM
Does government spending cause inflation? See how waste, crowding out, and stimulus spending quietly push prices higher over time. -
What Happens to Interest Rates During a Recession
Jan 08, 26 05:31 PM
What happens to interest rates during a recession? Explore why rates often fall, when they don’t, and how inflation, policy, and markets interact. -
Circular Flow Diagram in Economics: How Money Flows
Jan 03, 26 04:57 AM
See how money flows through the economy using the circular flow diagram, and how spending, saving, and policy shape real economic outcomes. -
What Happens to House Prices During Stagflation?
Jan 02, 26 09:39 AM
Discover how house prices and real estate behave during stagflation, with historical examples and key factors shaping the housing market.